A NEW METHOD OF SOLVING INITIAL BOUNDARY-VALUE PROBLEMS - Zbigniew Turek

ZTUREK Research-Scientific Institute
Warsaw , Poland

There are some useful methods of solving linear initial boundary-value problems in partial differential equations. One of them is the method of seperation of variables, called the Fourier method [1]. It consists first of finding solutions to the corresponding eigenvalue problem for functions of spatial variables and next solving ordinary differential equations for functions of time variable only. Each function of the eigenvalue problem satisfies prescribed boundary conditions. Finally the solution to the initial boundary-value problem is represented by an infinite series of these functions.

In paper [2] solving the heat conduction equation with non-Dirichlet boundary conditions, it has been shown that the solution to the problem can be represented with an arbitrary accuracy, by the Fourier cosine series

 

whose spatial components do not satisfy the boundary conditions given. The Fourier coefficients are calculated from a corresponding Infinite Set of Ordinary Differential Equations (ISODE) of the form:

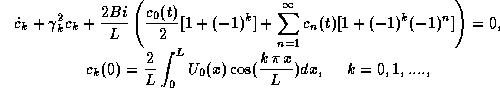
where is the initial condition and Bi is the Biot number. In paper [3] we prove that the Fourier cosine series (1) is a weak solution to the problem considered, which is the solution to the so called Integro-Differential-Boundary Equations [2,3]. The way how to get the IDBEs and ISODE is shown in [2,3].

Mathematical grounds as well as mathematical generalisation of the method is the subject of the present paper.

References:

[1]. R. V. Churchill, J. W. Brown, Fourier series and boundary value problems, McGraw-Hill Book Company, New Jork, 1978.

[2]. Z. Turek, A new method of finding approximate solutions to the heat conduction equation, Engng. Trans., 44, (2), 295-301, 1996.

[3]. Z. Turek, Application of the Fourier Cosine Series to the Approximation of Solutions to Initial non-Dirichlet Boundary-Value Problems, submitted for publication in Archives of Mechanics.