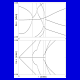
 Fig. 1. The real
and the imaginary part of the slowness s for bismuth
germanium oxide (Euler angles: 24, 70, 10 degrees).
Fig. 1. The real
and the imaginary part of the slowness s for bismuth
germanium oxide (Euler angles: 24, 70, 10 degrees). The surface acoustic wave amplitudes at the boundary of a piezoelectric half-space satisfy a matrix relation which is characteristic of the medium. The elements of the matrix are functions of slowness. In the paper, the singularities of the matrix are investigated at cutoff points of bulk waves. An approximated formula is derived for the matrix in the neighborhood of the greatest cutoff point, which also takes into account the singularity related to the Rayleigh wave.
Among elements of the matrix, one is of particular importance in the theory of surface waves in piezoelectrics. This element is equal to the ratio of the x component of the electric field and the z component of the electric displacement at the boundary. (The wave propagates in the x direction, and the z axis is normal to the boundary.) The ratio is a complex-valued function Z(r), where r is the x component of the slowness (the z component of the slowness is s).
The results of numerical calculations of the exact and the approximated function Z(r) are presented for several piezoelectrics.
 Fig. 1. The real
and the imaginary part of the slowness s for bismuth
germanium oxide (Euler angles: 24, 70, 10 degrees).
Fig. 1. The real
and the imaginary part of the slowness s for bismuth
germanium oxide (Euler angles: 24, 70, 10 degrees).
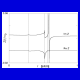 Fig. 2. The
function Z(r) for bismuth germanium oxide (Euler angles:
24, 70, 10 degrees).
Fig. 2. The
function Z(r) for bismuth germanium oxide (Euler angles:
24, 70, 10 degrees).
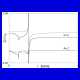 Fig. 3. The
function Z(r) (exact and approximated) for lithium niobate
(Euler angles: 0, 90, 90 degrees).
Fig. 3. The
function Z(r) (exact and approximated) for lithium niobate
(Euler angles: 0, 90, 90 degrees).
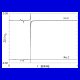 Fig. 4. The
function Z(r) (exact and approximated) for quartz (Euler
angles: 0, 90, 0 degrees).
Fig. 4. The
function Z(r) (exact and approximated) for quartz (Euler
angles: 0, 90, 0 degrees).
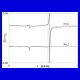 Fig. 5. The
function Z(r) (exact and approximated) for bismuth
germanium oxide (Euler angles: 0, 0, 45 degrees).
Fig. 5. The
function Z(r) (exact and approximated) for bismuth
germanium oxide (Euler angles: 0, 0, 45 degrees).
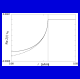 Fig. 6. The real
part of the function Z(r) (exact and approximated) for
bismuth germanium oxide (Euler angles: 0, 0, 45 degrees) in the
neighborhood of the cutoff point of bulk waves.
Fig. 6. The real
part of the function Z(r) (exact and approximated) for
bismuth germanium oxide (Euler angles: 0, 0, 45 degrees) in the
neighborhood of the cutoff point of bulk waves.