Strong chain extension and molecular orientation produced under high stresses has been considered for biaxial (thermoforming, film blowing) and uniaxial (fibre spinning) deformation of solid and liquid polymers [1-4]. Non-linear molecular orientation at high biaxial deformation of non-Gaussian chain molecules in a solid state is considered as directly related to the applied deformation [1] and steady biaxial extensional flow in a liquid state [2]. Equilibrium segmental orientation and stresses are considered using non-Gaussian inverse Langevin chain statistics with a Padé approximation. Closed-formula models are derived for solids and liquids. Global molecular anisotropy stress anisotropy are characterized. The approach is free from the limitations related to finite chain extensibility and slow convergence of the series expansion formulations at higher chain deformations. Non-linear stress-orientation behavior is discussed for biaxial, calendaring and uniaxial deformations [1]. Stress-orientation behavior in the biaxial elongational flow is discussed in a wide range of the elongation rates [2].

Transient distributions of non-Gaussian chain macromolecules in non-linear polymer fluids subjected to biaxial and uniaxial deformation are determined [3,4]. Numerical and self-consistent analytical method of solving the system of evolution equations are proposed. The non-linear model covers entire range of deformation rates and predicts molecular deformation asymptotically converging to the equilibrium chain deformation in the limit of infinite time scaled by a relaxation time. For slow deformation process, linear Gaussian model serves as a good approximation, while for very fast processes - solid-like behavior takes place with minor deviation between the molecular and macroscopic deformations, up to the level of full chain extension.

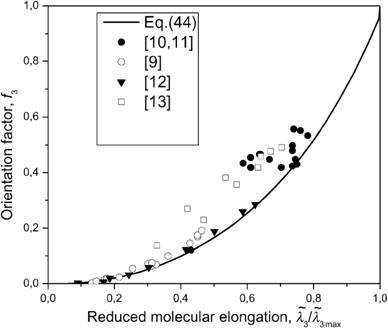
Calculated axial orientation factor vs. reduced molecular elongation coefficient (line) and experimental points [4].

[1]. Jarecki L., Ziabicki A., Development of molecular orientation and stress in biaxially deformed polymers. I. Affine deformation in a solid state, POLYMER, 43, 2549-2559, 2002.

[2]. Jarecki L., Ziabicki A., Molecular orientation and stress in biaxially deformed polymers. II. Steady potential flow, POLYMER, 43, 4063-4071, 2002.

[3]. Ziabicki A., Jarecki L., Schoene A., Transient biaxial orientation of flexible polymer chains in a wide range of deformation conditions, POLYMER, 45, 5737-5742, 2004.

[4]. Schoene A., Ziabicki A., Jarecki L., Transient uniaxial orientation of flexible polymer chains in a wide range of elongation rates, POLYMER, 46, 3927-3935, 2005.