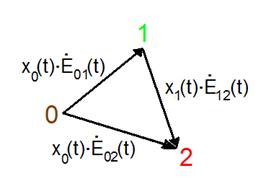
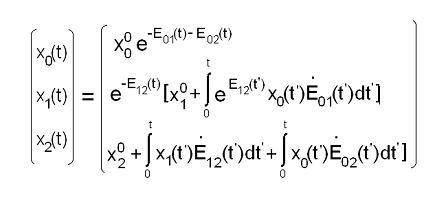Understanding of the kinetic mechanisms governing development of lamellar thickness distribution is under the scope of publications [1,2] and creation/disappearance of polymorphic phases during crystallization is the subject of papers [3-7].

An unique mathematical model of development of thickness distribution of lamellar crystals during crystallization from the polymer melt has been proposed [1]. The model can be used to predict or design the thickness distribution of crystals by adjusting thermal conditions and crystallization time, without the need of synchrotron measurements. Continuity equation for the lamellar thickness distribution is proposed and solved. The model accounts for fast creation of doubled crystals during a “doubling time” and slow logarithmic thickening subsequent to the doubling transformation. The approach concerns crystallization in systems without mesophase involved in the transformation. It was also shown that the thicknesses range of plate-like crystals created during crystallization is limited depending upon crystallization temperature [2].

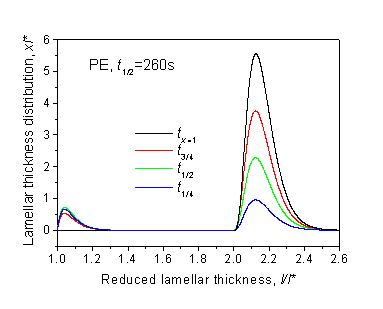
Development of lamellar thickness distribution at consecutive conversion times (indicated) computed for isothermal crystallization of PE at 123^oC[1].

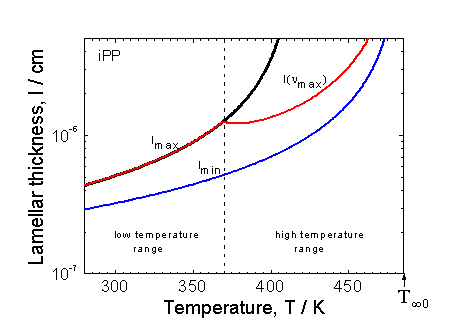
A map of nucleation behaviour for plate-like crystallization [2].

Fundamentals of a kinetic model of multiphase polymorphic crystallization proposed by professor Andrzej Ziabicki [3] has been developed [4-6] and applied [7]. Using the model, three-phase system composed of an amorphous component and two polymorphic solid phases has been considered. The approach predicts development of the phase composition under different thermal conditions. It was shown, how the modification of material characteristics affect on polymorphic crystallization kinetics [5] and how proportions between polymorphic phases can be regulated by the change of concentration of predetermined nuclei and temperature [6]. Limited degree of crystallization which results from molecular constrains in polymer systems is introduced in the model.

Phase transitions and development of the phase composition in a three-phase system [4].

[1]. Jarecki L., Misztal-Faraj B., Kinetic model of polymer crystallization with the lamellar thickness distribution, EUROPEAN POLYMER JOURNAL, 73, 175-190, 2015.

[2]. Misztal-Faraj B., A simple model of plate-like crystallization with constant plate thickness, JOURNAL OF MATERIALS RESEARCH, 28, 1224-1238, 2013.

[3]. Ziabicki A., Nucleation-controlled multiphase transitions, JOURNAL OF CHEMICAL PHYSICS, 123, 174103-1-174103-11, 2005.

[4]. Ziabicki A., Misztal-Faraj B., Modeling of phase transitions in three-phase polymorphic systems: Part I. Basic equations and example simulation, JOURNAL OF MATERIALS RESEARCH, 26, 1585-1595, 2011.

[5]. Misztal-Faraj B., Ziabicki A., Modeling of phase transitions in three-phase polymorphic systems: Part II. Effects of material characteristics on transition rates, JOURNAL OF MATERIALS RESEARCH, 26, 1596-1604, 2011.

[6]. Misztal-Faraj B., Ziabicki A., Effects of predetermined nuclei and limited transformation on polymorphic crystallization in a model polymer, JOURNAL OF APPLIED POLYMER SCIENCE, 125, 4243-4251, 2012.

[7]. Sajkiewicz P., Gradys A., Ziabicki A., Misztal-Faraj B., On the metastability of beta phase in isotactic polypropylene: Experiments and numerical simulation, E-POLYMERS, No.124, 1-20, 2010.